Corrosion of reinforcement in HVFA concrete - II

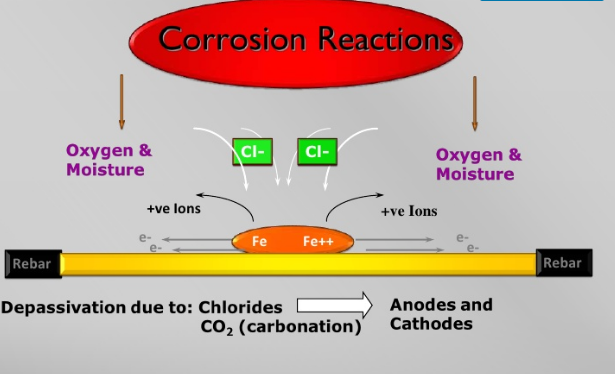
The stages of rebar corrosion

A careful illustration survey for any sign of cracking, spalling and rust staining provides important information as to whether the corrosion of reinforced steel is really a cause of concern or is there some other cause of distress. Usually half-cell potential(Ecorr), concrete resistivity (ρ), and corrosion current density (Icorr) are the three major measure parameters which are connected with the degree of reinforcement corrosion. While Half-cell potential (Ecorr) and concrete resistivity(ρ) is a qualitative index while the corrosion current density(Icorr) is a quantitative index. Among all the methods of Icorr the ‘linear polarization method’ is best, simplest, non-destructive, fastest, relatively inexpensive and most widely used. However, the main difficulties observed were: the high resistance of concrete between the working electrode (rebar) and the reference electrode offers a latent drop; the distribution of the electrical signal applied for polarization of rebar is non-uniform all through the cross-section of beam and accuracy of Tafel constant.

Keeping the above difficulties, experts Ahmad and Bhattacharya suggested an understanding and calculation procedure, for in situ measurement of Ecorr, ρ and Icorr of rebar implanted in the concrete. Using the above observation, the ohmic resistance and resistivity of concrete, the polarization resistance of rebar, Tafel slopes and corrosion rate can be determined. The time required for corrosion beginning depends on the time required for CO2 or Cl−ions to disperse to the steel-to-concrete interface and activate corrosion. Extensive research work has been devoted to develop the models that help to predict the time for corrosion initiation. Different models are validated in the field studies, for the rate of Degree of Corrosion carbonation propagation and chloride entrance which predict the time for corrosion initiation can be found in literature. However, Bazant suggested a mathematical model to calculate the time between the corrosion initiation and corrosion cracking of RC bridge decks. Bazant’s model assume that all corrosion products create pressure on surrounding concrete and related the duration of steady-state corrosion period (tcor) as follows:

tcor = ρcor (DΔD/pJr)

Here: ρcor is combined density factor for steel and rust, D is diameter of rebar, ΔD is augment in diameter of rebar due to rust formation, p is the perimeter of rebar, Jr is immediate corrosion rate given as:

Jr = (W/F)Icorr

Where:

Jr = instantaneous corrosion rate (gm/cm2/s)

W = equivalent weight of steel = 55.85/2 = 27.925 gm

F = Faraday’s constant = 96487 C

Pr = penetration rate (cm/s)

After the Bazant's work there were some extensions done by Liu and Weyers taking same parameters as used in Bazant’s model along with time necessary for corrosion products to fill a porous zone around the re bar prior to creating an internal pressure on surrounding concrete. In Liu and Weyers model, the rate of steel mass loss was assumed to be directly comparative to the square root of the product of the corrosion current and the time of corrosion contact. This assumption significantly underestimates the amount of steel weight loss compared with that obtained by Faraday’s law, consequently overestimating the time to corrosion cracking.

Morinaga proposed the following empirical equation based on the field and laboratory data to forecast the time from corrosion initiation to corrosion cracking (tcr):

 tcr = [0.602D{1+2(C/D)}0.85]/icor

where: tcr is time from corrosion initiation to corrosion cracking(days), D is the rebar diameter (mm), C is the clear concrete cover(mm), and icor is the corrosion rate (10-4 g/cm2 )day). Empirical equation proposed by Morinaga does not consider the mechanical properties of concrete which may significantly affect the time of corrosion.

Considering the primary deficiencies of the previous models, Maaddawy and Soudki [presented a mathematical model in which a relationship between the steel mass loss and the internal radial pressure caused by corrosion was developed accounting the mechanical properties of concrete. According to it, the time from corrosion initiation to corrosion cracking, tcr is given as

tcr = [7117.5(D+2δ0)(1+υ+ψ)/iEef][(2Cfct/D)+ 2δ0Eef/{(1+υ+ψ)(D+2δ0)}]

where: ψ = D/2/2C(C+D/), D/ = D+2δ0, and Ecf (effective elastic modulus of concrete) = [Ec /(1+ϕcr)] in which Ec is elastic modulus of concrete and ϕcr is concrete creep coefficient, D is the diameter of rebar(mm), δ0 is width of porous zone typically in a range of 10–20μm, υ is Poisson’s ratio of concrete (0.18), C is clear concrete cover (mm) and i is current density. Eqs.  and  may be used to calculate tensile strength and Young’s Modulus of concrete where fc / is characteristic strength of concrete

fct = 0.94√fc/ MPa

Ec = 4500√fc/ MPa